아자!

출처 : http://blog.naver.com/elsacred/50015540325

0. 들어가며

드디어 게으름을 떨치고 tangent space 에 대해서 정리해 봅니다.

이사도 했고 좀 더 여유가 생길 것 같습니다. 이제 좀 열심히 해 볼까 합니다.

픽셀 당 조명을 다루면서 탄젠트 공간에 대해 다루겠다고 이야기했었습니다.

저도 잘 모르지만 한 번 정리해 보도록 하겠습니다.

1. What is tangent space?

만약 우리가 구(sphere)인 메시를 가지고 있고 각 정점의 법선을 알고 있다고 할 때, 이것을 (텍스처) 평면상에 펼친다면 어떨까요. 각 점에서는 수직인 벡터들이었지만 평면에서 볼때는 위쪽을 가리키지 않고 서로 다른 방향을 가리키게 될 것입니다.

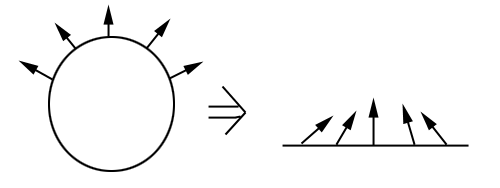
하지만 일관성을 위해서 평면으로 펼친 모든 normal 벡터가 위쪽을 바라보게 만든다면 어떻게 될까요. 그렇게 되면 각 점의 normal 벡터를 수직축으로 하는 좌표계가 생성이 됩니다.

normal(법선) 벡터는 어떠한 면에 수직인 벡터이며, bi-normal(종법선) 벡터는 이 normal 에 수직인 벡터입니다. 어떤 벡터 A, B, N 이 있을 때 T X B = N 인 관계의 두 벡터 A, B 를 접선이라고 합니다. X 는 외적기호구요. 이때 B 를 bi-normal 이라고 하면 T 를 tangent 라고 할 수 있습니다. 즉 T 와 B 는 같은 평면상에 존재하는 벡터라는 것을 알 수 있습니다.

즉 tangent space 라는 것은 오브젝트 공간에 있는 어떤 점의 normal 을 수직축으로 하는 공간이라고 할 수 있습니다.

탄젠트 공간을 개념도로 표현해 보면 아래와 같습니다.

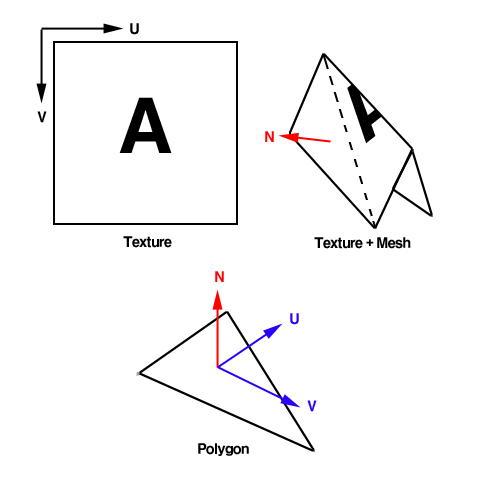
2. How to calculate tangent space

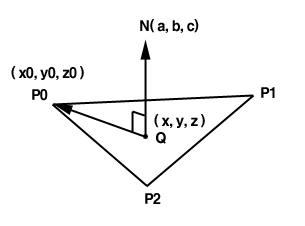
Q -> P0 를 P' 라고 할 때, P' 와 N 은 수직입니다. 이것이 의미하는 바는 둘을 내적한 결과가 0 이 나온다는 것입니다. 그렇다면 다음과 같은 평면 방정식을 유도할 수 있습니다.

dot( P', N ) = 0 -------------------------------- 1)

p' = ( ( x0 - x ), ( y0 - y ), ( z0 - z ) ) -------------------------------- 2)

N = ( a, b, c ) -------------------------------- 3)

dot( P', N ) = ( x0 - x )a + ( y0 - y )b + ( z0 - z )c -------------------------------- 2), 3) 에 의해

-( ax + by + cz ) + ( ax0 + by0 + cz0 ) = 0 -------------------------------- 1) 에 의해

ax + by + cz - ( ax0 + by0 + cz0 ) = 0 -------------------------------- 양변에 -1 곱함

a, b, c, x0, y0, z0 을 알고 있으므로 - ( ax0 + by0 + cz0 ) 은 상수이며 이를 D라 표현합니다.

ax + by + cz + D = 0 --------------------------------- 결론)

이 평면 방정식은 오브젝트 공간의 XYZ 축을 이용해 평면 위에서의 어떤 점의 좌표를 표현한 것입니다.

'평면' 이라는 단어를 통해서 약간이 느낌이 오실 겁니다. 우리는 오브젝트 공간의 어떤 벡터( normal )를 탄젠트(텍스처) 공간으로 옮기려고 하고 있습니다. 그렇다면 XYZ 관계 축으로 구성된 공간을 UNV 관계 축으로 구성된 공간으로 표현해야 한다는 것을 알 수 있습니다.

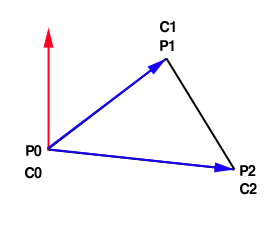
2.2. Drive a 3x3 matrix for tangent space

이제 개념적으로 탄젠트 공간이라는 것이 대충 이해가 가실테지만 문제는 여기부터입니다. 우리는 텍스처( normal map ) 에 normal 을 저장하게 됩니다. 이 때 그 값을 기울기( gradient )라는 용어로 표현을 많이 합니다. 기울기값은 당연히 오브젝트 공간의 normal 을 탄젠트 공간의 normal 로 저장한 값을 의미합니다.

1. 탄젠트 공간이란?

우리 지구본이 있다고 하자. 그리고 이 지구본을 쫙 펼쳐 지도를 만들었다고 하자. 그런데 갑지가 다시 지구본이 필요해져 지도를 다시 지구본으로 만들어야 한다고 하자. 이 경우 우리는 어떻게 하면 지구본을 다시 만들 수 있을까?

비록 완벽하게 대응되는 것은 아니지만 위의예가 탄젠트 공간이 필요한 이유를 가장 잘 설명해 줄 수 있다. 만약 우리가 어떠한 3차원 물체를 2차원 평면으로 만들었다면, 우리는 이 2차원 평면을 바탕으로 3차원의 물체를 절대로 만들 수 없다. 하지만 3차원 물체를 2차원 평면으로 변환할때, 2차원 평면의 각 점에 그것이 3차원에서 가졌던 어떠한 정보를 저장해 두었다면 어떠한가? 이 경우 우리는 어떻게든 2차원 평면을 다시 3차원 물체로 복원할 수 있게 될 것이다. 여기서 말하는 어떠한 정보가 바로 탄젠트 space이다.

2. 탄젠트 공간의 정의

3차원 공간의 탄젠트 공간은 다음의 세 벡터를 축으로 하는 공간이다.

1) 한 점의 법선 벡터

2) 한 점의 접선(탄젠트) 벡터

3) 바이노멀 벡터 : 법선 벡터와 접선 벡터를 외적하면 구해지는 벡터

일반적으로 tangent space는 원래의 공간과 같은 차원을 가지며, 한 점에서 생성 가능한 모든 접선 벡터를 포함한다. 가령 위 그림의 경우, 접선 벡터와 바이노멀 벡터가 생성하는 평면은 가능한 모든 접선 벡터를 포함한다. 여기서 주의할 점은 tangent space의 개념은 비단 3차원 공간만이아닌 임의의 차원의 공간에 대해서도 적용될 수 있다는 점이다.

3. 탄젠트 번들

또한 모든 tangent space들은 2배의 dimension을 갖는 새로운 공간을 생성하기 위해 서로 붙여질 수 있는데(“glued together”), 이를 가능하게 해주는 것이 바로 tangent bundle의 개념이다. 이에대한 개념은 형태학 및 manifold등의 개념을 이해하여야 하므로 자세한 설명은 생략 하기로 한다.

4. 왜 사인, 코사인이 아닌 탄젠트를 이용하는가?

한점의 기울기를 가장 직관적으로 구할 수 있는 것이 다름아닌 탄젠트 이기 때문이다.

가령, 우리가 한 점의 기울기를 구해야 한다고 하자. 우리는 일반적으로 먼저 한 점의 접선을 빗변으로 하는 직각 삼각형을 생성하여야 하고, 그 직각 삼각형의 '높이/밑변' 으로 기울기를 구해주게 된다. 그런데 이 기울기는 바로 직각 삼각형의 빗변에 대응하는 각도의 탄젠트 값이다. 즉 탄젠트(빗변의 대응각)가 곧 기울기란 말이다. 때문에 한점의 기울기가 탄젠트라 불리기도 하는 것이다.