안녕하세요? 강좌도 작게 작게 많이 하려고 준비한 강좌이니 만큼,
댓글수에 연연하지 않고 쾌속으로 나가도록 하겠습니다!!

오늘 하루... 최대한 올려보죠 ㅋㅋ

*이 강좌는 C언어를 끝냈다는 가정하에 실시합니다.

 ┌───────────────┐
---앞으로의 목차---
2. 함수 오버로딩
3. 디폴트 매개 변수
4. 인-라인(inline)함수
└───────────────┘
<지난 강좌를 살펴보고 와주세요 !! : http://blog.naver.com/owndks98o/120155673402 >

1-2. 함수 오버로딩(Function Overloading)

C언어를 배우면서 프로그래밍이란 것에 어느덧 관심이 가길 시작했던 부분이 언제였을까요?
아마도 내 입맛대로 디자인 할수 있는 함수를 배우면서 일것이라 생각합니다. 저역시 그러했고요.
C++에서는 C보다 더욱 넓은 함수의 기능을 제공합니다.
알아볼까요?

void func(void){}     //ㄱ.
void func(int a){}    //ㄴ.
void func(char c){} //ㄷ.

이런, 전혀 쓸데없는 함수 3가지가 있다고 가정해 봅시다.
하지만 이런 소스는 C언어에선 분명 문제가 있습니다.
바로 같은 이름의 함수가 선언되었다는 것이죠.

하지만 C++에서는 다르게 생각해 봐야 할 부분일 것입니다.
이 소스의 메인함수가 아래와 같이 정의되어 있을때,

int main(){
func();      //1번
func(10);   //2번
func('a');  //3번
reuturn 0;
}

당연히 여러분은,
1번함수는 위의 'ㄱ'에 해당하며, 
2번함수는 위의 'ㄴ'에 해당하며,
3번함수는 위의 'ㄷ'에 해당한다는 사실을 알 것이라 생각합니다.

바로 이것이 C++의 아이디어, 함수 오버로딩 입니다.

따라서, 함수오버로딩이란, 함수명은 같으나 인자의 타입이나 수가 다른 함수의 선언을 허용하는 것 을 일컫습니다.

함수 오버로딩의 조건은 정말로 간단합니다.
"인자의 갯수가 다르거나, 타입이 다르거나!"
간단하죠?

아래의 소스는 함수 오버로딩을 보여주고 있습니다.

/*
Function Overloading.cpp
*/

#include

void func(){
std::cout<<"FUNC 1 CALLED"<
}

void func(int a){
std::cout<
}

int main(){
func();
func(10);
return 0;
}

그렇다면 만약, 리턴값이 다르면 어떻게 될까요?

void func(){}
int func(){return 10;}

위와 같이 인자값,함수명은 같으며 리턴값이 다른 함수가 있습니다. 과연 함수오버로딩은 성립할까요?

int main(){
func();
return 0;
}

답은 X입니다.
위의 메인함수를 보면 도무지 무엇을 호출했는지 감이 잡히지 않죠.

오해하지 않으시길 바랍니다.

그럼 다음강(1-3)에서는 디폴트 매개변수를 알아보죠!


저작자표시 비영리 (새창열림)



[출처] [C++ 강좌] - 1-1.달라진 입출력 -|작성자 leanix




안녕하세요? leanix입니다!
이제부터 C++에 대한 강좌를 시작할 것이며, 많은 것을 알아가셨으면 하는 마음을 가지고 시작합니다.

강좌에 나온 모든 예제는 컴파일후, 소스와 프로그램을 올리겠습니다.

*C언어를 배우셨다는 전제하에 실시합니다.

┌───────────────┐
---앞으로의 목차---
1. 달라진 입출력
2. 함수 오버로딩
3. 디폴트 매개 변수
└───────────────┘

1-1. 달라진 입출력

C언어를 배우며 제일 처음 접해본 프로그램이 아마, HelloWorld.exe 였을 것이라 생각합니다.

#include

int main(){
printf("Hello World!");
return 0;
}

이런 간결하고도 간결한 코드였죠.
C++에서도 마찬가지로 C++스타일의 Hello Word 를 작성하는 것으로 그 장대한 시작을 울려봅시다!

/*
HelloWorld.cpp
.cpp 를 사용하셔야 합니다. C++의 문법을 적용시키기 위함입니다.
*/

#include

int main(){
std::cout<<"Hello World"<
std::cout<<'A'<<123<
return 0;
}

이것이 C++의 출력의 기본입니다.
C++에서는,
iostream 헤더를 포함시킵니다.
std::cout<<출력할것  의 형식으로 출력을 합니다.
std::endl은 한줄을 넘기는 의미를 지닌다.(=\n)(endline의 약자)
std::cout<<출력1<<출력2; 등의 형식으로 이어쓸수 있다.
간단하죠??

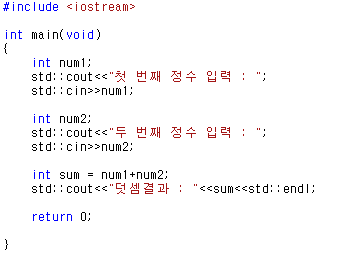
그렇다면 이번에는 C++스타일의 입력을 알아봅시다.

/*
Plus.exe
*/

#include

int main(){
int v1,v2;

std::cout<<"1번쨰 숫자입력 : ";
std::cin>>v1;

std::cout<<"2번째 숫자입력 : ";
std::cin>>v2;

int result=v1+v2;
std::cout<<"덧셈 : "<
return 0;
}

그렇게 어렵지 않아 보입니다.
std::cin>>변수  의 형식을 통해 값을 입력받습니다.
역시, std::cin>>변수1>>변수2; 의 형식을 취할수 있습니다.
C와는 다르게, 변수의 선언이 앞부분 뿐만이 아닌, 어디서도 할수 있습니다.
이것이 printf, scanf를 대신하는 C++의 다입니다! 간단하죠??

덤으로, C++에서는

int i;
for(i=0; i<10; i++){...}

같은 코드를,

for(int i=0; i<10; i++){...}

처럼 줄일수 있습니다.

또한 Visual Studio 7.0 이상부터는 지역변수로 인정이 되어서,

for(int i=0; i<10; i++){
std::cout<
}
int i;

처럼 변수를 두번 선언하는 코드도 상관이 없답니다!!

그럼 다음강(1-2) 에서는 함수 오버로딩에 대해 알아봅시다!!
[출처] [C++ 강좌] - 1-1.달라진 입출력 -|작성자 leanix












저작자표시 비영리 (새창열림)



[1] 문자열 출력

C언어 출력 함수는 printf 입력 함수는 scanf 함수등이 있었다.

우선 설명하기전에 예제를 하나보고 분석해보도록 하겠습니다.

꼭 직접 컴파일러에 입력해보시기 바랍니다.! (단! 파일의 이름을 지정할때 확장자는 반드시

.cpp로 지정해주셔야 C++문법규칙을 적용한 C++컴파일로 컴파일이 될수 있습니다.)

컴파일러 설치및 실행방법은 ( http://blog.naver.com/net_zhdk/120149784643 ) 여기나

아니면 인터넷에 직접 검색하는것이 좋습니다.!


실행 결과

위의 예제 소스코드를 자세히 보면 출력에 관한 몇가지 사실을 알 수 있다.

우선 이해하지말고 살펴보기만 하자.

* 헤더파일 선언 #include
* std::cout<< 를 이용한 출력
* std::endl 를 이용한 줄바꿈(개행)
우선 이 3가지에 대해 알아보도록 하겠습니다.

[1-1] 헤더파일 선언 #include

C언어 배우신분들은 알겠지만. C언어에서 printf 출력함수를 사용할려면 #include

이 헤더파일을 추가 해줘야만 printf함수를 사용할 수 있다.

이와 똑같이 C++언어 에서 출력하기 위해서는 #include 헤더파일을 선언해줘야 한다.

근때 강좌를 읽는분들은 이런 질문이나 생각을 할 수 도 있다.

왜 C언어 에서는 stdio.h 헤더파일 h 확장자를 붙여줫는데 C++언어 에는 그냥 iostream인가요?

맞는 말이다 ! 하지만 헤더파일 확장자는 C언어와 마찬가지로 .h 이다. 그렇지만 C++에서는

프로그래머가 만든 헤더파일이 아닌 이상, 즉 표준 헤더 파일선언에는 확장자를 않붙여주기로

약속을 했다.! 과거 C++에는 붙여줫지만 새로운 표준 라이브러리에는 확장자를

떼어 줫다.!

[1-2] std::cout<< 를 이용한 출력

위 예제에서는 뭔가를 출력하기 위해 std::cout<< 라는 문장을 사용햇었다.

사용방법은 이렇다.!

std::cout<<"출력대상";

"출력대상" 이 위치에는 무엇이든 올수 있다. 정수 또는 실수 또는 문자 문자열 공백 변수도

올수있다. C언어에서는 변수에 담긴 값들을 출력할려면 서식문자를 지정해줘야만 햇는데

C++에서는 데이터 성격에 따라 출력이 이뤄진다. 조금씩 알아가고 있지만..

아직은 정확히 모든것을 알 수 없다.. 앞으로 공부하면서 천천히 다 알게 될껏이다.

[1-3] std::endl 를 이용한 줄바꿈(개행)

그리고 자세히 문자을 보면 << 연산자가 있다. 사실 이것도 연산자 이다. 이 연산자를 이용하면

둘 이상 출력대상을 연이어 지정해줄 수 있다.

std::cout<<"출력대상1"<<"출력대상2"<<;

즉, << 연산자는 둘 이상의 데이터 출력을 할때 쓰이는 연산자이다.

그리고 std::endl 문장은 개행이다. C언어에서는 특수문자(이스케이프 시퀀스) 문자열 끝에 \n를

사용햇지만 C++에서는 std::endl 를 사용하여 문자열을 개행을 한다.


[2] 데이터 입력

이번에는 키보드로부터 뭔가를 입력 할 때 쓰이는 것들을 알아보도록 하겠다.

C언어에서는 입력함수 대표적인 scanf함수가 있었다.

그럼 C++에는 std::cin>> 이 있다.

이번에도 먼저 예제를 입력해보면서 분석해보도록 하자.


실행결과


위의 예제를 살펴보면 두가지 사실을 알수 있다.

* 키보드로부터의 데이터 입력에는 std::cin 과 >> 연산자가 사용된다.
* C++ 언어의 변수 선언은 어디서든 가능하다.

[2-1] 키보드로부터의 데이터 입력에는 std::cin 과 >> 연산자가 사용된다.

위의 예제에 보이듯이 키보드로부터 뭔가의 데이터를 입력받을려면 이렇게 해야 된다.

std::cin>>입력변수;

입력변수 의 위치에는 데이터의 값을 저장할 변수이름이 오면 된다.

그리고 더불어 C++에서도 서식문자 지정을 않해줘도 된다.

[2-2] C++언어의 변수 선언은 어디서든 가능하다.

C언어에서 프로그램 작성할때 변수 선언은 함수 안에서 제일 먼저 등장 해야 햇다.

하지만 C++언어 에서는 함수 내 어디 위치든 변수 선언이 가능하다.

그리고 한 가지 더 std::cout<<"출력대상1"<<"출력대상2"; 와 같이..

입력 std::cin>> 도 여러가지 입력변수를 지정할수 있다.

std::cint>>입력변수1>>입력변수2; 이렇게


저작자표시 비영리 (새창열림)





일부 사진은 클릭하면 영상이 나옵니다.


원문 링크는

http://game.watch.impress.co.jp/docs/series/3dcg/20120314_518785.html

를 참조 하세요


【GDC 2012】니시카와 젠지의 3D 게임 팬을 위한「inFamous 2」강좌
훌륭하지만 아직은 불완전한 SSAO。그 약점을 보완하는 기술에 주목!!



3월5일~ 9일 개최（현지 시간）
장소：San Francisco Moscone Center


3D게임 그래픽스의 커다란 테마로 [음(陰)]과 [영(影)]이 있다. 최근에 [그림자(影)]생성은 Depth Shadow Map 기법이 주류이며, 그림자(影)생성을 위한 섀도우 맵을 여러장 사용하여 그것들을 시점으로부터의 원근에 따라 할당하는 캐스케이드 확장 기법이 주류로 되고 있다. 이러한 어프로치의 그림자(影) 생성은 생성하는 섀도우 맵의 해상도에 의존한 정밀도가 되며, 미세한 그림자(影)를 만들어낼 수 없다.

또 간접광등의 2차광원으로부터의 그림자(影)생성은 현재 쓰이고 있는 방식중에는 절망적이다.
여기서 최근 각광을 받아 온것이 렌더링 결과에 따라 출력되는 Depth(심도)버퍼의 내용을 바탕으로하여
포스트 프로세스 방식의 가상적인 환경광에 대한 그늘(陰)을 생성하는 SSAO(Screen Space Ambient Occlusion)이다

SSAO는 Crytek에 의해 고안되었으며 눈깜빡할 사이에 여러 타이틀에 채택되었지만 그와 동시에 자잘한 문제가 부각되어 왔다. 최근 GDC에서는 이 SSAO의 개량에 관련된 세션이 많이 생겼으며 올해도 예외 는 없었다。「Ambient Occlusion Fields and Decals in Infamous 2」도 그 세션중에 하나 였다. 매우 이해하기 쉬웠고 게다가 구현이 간단해보이니 소개하고 싶다。

【inFamous 2】


■　Screen Space Ambient Occlusion（SSAO）는 완벽하지 않다!


Nathan Reed氏(Rendering Programmer、Sucker Punch Productions)
PS3 전용 타이틀인「inFAMOUS 2（인퍼머스 2）」에서는 새겨넣는 형태의 그림자[陰] 로써 버텍스 단위로 차기차폐 상태를 새겨넣는 고전적인 AO(Ambient Occlusion)와 SSAO 양쪽을 사용하여 다양하고 풍부한 "그림자(陰)" 표현을 하였다.

버텍스 단위의 AO와 SSAO는 각각의 단점과 장점을 서로 감싸는 좋은 보완관계가 성립된다. 버텍스 단위의 AO는 움직이지 않는 정적인 오브젝트 그것도 거대한 건물이 만들어내는 대국적인 그림자( 陰(影)) 생성에는 유효하다

이 그림자(陰(影))의 투영되는 곳의 버텍스를 미리 세세하게 해두지 않으면 안되는 귀찮음이 있지만 SSAO에서는 만들기 어려운 광범위의 그림자((陰(影)))를 만들어 내는데에 적합하다. 이것을 보간하는 존재가 SSAO이다

SSAO는 정적인 오브젝트는 물론, 돌아다니는 동적인 오브젝트에 대해서 국소적인 그림자((陰(影))) 생성을 수행할 수 있다. 구체적인 알고리즘은 아래와 같다.


보고 있는 픽셀이 어느정도 차폐되고 있는 장소의 픽셀인가를 , 그 픽셀에 대응하는 Z값과 그 픽셀 주변에 대응하는 Z값을 읽어들여, 그 값 끼리 비교해서 구한다. 그 비교 연산으로부터 깊이 맵(심도 맵)상의 깊숙히 닫혀진 장소에 있는 픽셀일수록 차폐도가 높다고 하고 "그림자(陰)"색을 입힌다.

간지나게 말하면 깊이맵 상에서 초 로컬한 레이캐스팅을 수행하여 차폐상태를 조사하는 수법이라고
할 수 있다.

하지만 SSAO는 결국은 렌더링 결과에 대해서 수행하는 화면좌표계 포스트 프로세스이기 때문에
몇가지 약점이 있다.

우선 렌더링 결과의 바깥둘레 부근은 (심도버퍼의)정보가 부족하기 때문에 차폐도를 제대로 계산 할 수 없다. 그림자색(陰色)이 엷어지는것 뿐이므로 무시되고있는 케이스가 대부분이다

또 깊이 맵은 시점으로부터 본 깊이 정보밖에 저장되어있지 않으므로 무언가에 차폐되고있는 가에 대한배후(背後)의 차폐도는 계산 할 수 없다.

그것과 씬이나 오브젝트에 대해서 시점까지의 거리가 거의 일정한 게임이라면 눈치채기 어렵지만
씬이나 오브젝트에 대해서 시점을 멀리하거나 가까이 하거나 하면 부자연스러운것을 눈치 채게 된다.

그렇다. SSAO에서 입혀진 그림자색(陰色)의 범위(크기)는 화면좌표계에서의 차폐도의 탐색이 수행되는것뿐이므로 그려지는 그림자색(陰色)의 영역은 화면상의 면적에 대해서 거의 일정하게 되버리는 것이다.

예를 들면, 어떤 막대 모양의 오브젝트의 밑부분에 그려진 그림자"陰"색의 크기에 주목을 하고 보면 그 오브젝트에 찰싹 붙을 정도로 가까이서 봐도 멀리 떨어져서 봐도 화면상에 그려지는 밑부분에 그림자(陰)의 크기는 변하지 않는다.

정확히는 가까이 갔을때는 그 막대의 빝부분이 확대해서 보이기 때문에 그 그림자 색(陰)은 크게 보여야 하며, 멀리 떨어졌을때에는 막대가 작게 보이기 때무문에 그것에 맞춰서 작게 보여야 한다


■　AO Fields 방식


「inFAMOUS 2」에서 AO Fields 방법
「inFAMOUS 2」는 3인칭 시점의 오픈 월드 형태의 액션 게임으로 비교적 카메라가 씬이나 오브젝트에 대해서 가까이 가거나 멀리가거나 할수있는 시스템으로 되어있다.

게다가 초능력을 사용하여 자동차같은 커다란 오브젝트를 집어 던지거나 이동시키거나 할 수 있기 때문에 위에서 말한 SSAO의 약점은 크리티컬하게 보이는 상황이 있다.


그래서「inFAMOUS 2」개발 팀은 SSAO를 독자적으로 연구하여 개량하기로 했다.
그중 하나가「Ambient Occlusion Fields」(AO Fields)이다.

이 방식에서는 각 오브젝트 모델에 짝이되는 AO Fields를 사전 계산을 할 필요가 있다.
AO Fields란 감각적으로 말하자면 [ 그 오브젝트가 모든 방향에서 어떤 다른물체들을 차폐하는 가 ] 라는 정보이다.

이 AO Fields의 크기는 각 오브젝트 모델을 완전히 가리는 직육면체보다도 더욱더 큰 직육면체 로 한다.
이 커다란 직육면체를 xyz 각 축 8~ 16분할하여 복셀로 분할하고 이 각 복셀의 중심으로부터 전방위(6방향)에 대해서 32 x 32텍셀의 큐브맵을 렌더링 한다.

【AO Fields】
AO Fields 이미지（왼쪽）、각 복셀에서의 AO Fields는 각 복셀의 중심으로부터 봤을때의 전방위의 배경을 큐브맵으로 렌더링한 결과로부터 얻는다（오른쪽）

여기까지는 꽤 대담하다. 렌더링 된 큐브맵을 탐색해서 그 중심을 구하고 복셀의 중심으로부터 이 중심으로의 방향을 산출한다. 이것을 차폐 벡터라고 한다. 참고로 여기서 말하는 [ 중심 ] 이라는 것은 큐브맵에 그려져 색칠된 텍셀의 면적으로부터 그 중심을 구하는것 뿐이다. 이것으로 이 복셀의 중심으로부터 본 [차폐 방향≒가장 이 지점이 차폐되고있는 방향]가 구해진다

이 큐브맵에 렌더링된 텍셀의 면적(칠해진 면적)은 이 복셀의 차폐율을 나타내고 있으며 이면적을 바탕으로 [ 이 지점의 차폐율 ]을 구한다.

이렇게 구한 차폐방향(x,y,z)와 차폐율을 텍스처에 저장한다. 차폐방향은 벡터이므로 RGB에 저장하고, 차폐율은 스칼라 이므로 α 채널에 저장한다. 이렇게 계산되었을때 가능한것이 3D 텍스처(3차원의 수치 테이블)로 이것이 그 오브젝트에 짝을 이루는 AO Fields라는 것이 된다.


【AO Fields의 사전계산】

「inFAMOUS 2」의 AO Fields 방식은 Mattias Malmer의 논문 「Fast Precomputed Ambient Occlusion for Proximity Shadows」을 참조하고 있으며, 이 논문을 참고로 AO Fields의 직육면체 사이즈가 결정되었다고 한다

세션에서는 실제「inFAMOUS 2」상의 오브젝트로 AO Fields를 어느정도의 크기로 잘랐는가도 구체적인 값을 알려주었다.

예를들면 자동차에서는 32 x 16 x 8 의 복셀로 구분지어 각 테이블이 32비트 정수였기에 3D텍스처의 용량은 16,384바이트(16KB)로 되어있다. 마찬가지로 공원의 의자는 16x8x8복셀로 4KB, 쓰레기통은 8x8x8 복셀로 2KB. 3D 텍스처라고 해도 꽤 엉성하기에 의외로 사이즈는 작다. 단 사이즈는 작지만 데이터 테이블은 벡터 데이터이며 정밀도가 요구되므로 텍스처 압축(DXT)는 하지 않았다는 것.

【AO Fields의 크기】
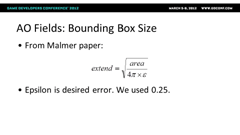「다른 물체의 미치는 차폐상태」를 구하므로 오브젝트 사이즈보다도 필연적으로 큰 영역이라고 생각할 필요가 있다. 그림의 회색 상자가 오브젝트를 감싸는 보정된 사이즈의 직육면체라고 했을때 파란 상자가 AO Fields。「inFAMOUS 2」에서는 참고논문을 본 떠ε=0.25를 선택했다


■　AO Fields를 사용한 렌더링


여기까지를 그대로 구현한 결과. 그림자색(陰色)엉성한 사각형이 되어 나타난다. 이대로는 너무 부자연스럽다
실제로 이 AO Fields를 런타임에서 어떻게 이용할까 인데 모든 오브젝트군의 렌더링이 끝난 후에 각 오브젝트의 AO Fields사이즈의 직육면체를 렌더링 해 나가는 형태이다.

라고는 해도 실제로 직육면체의 실체를 그리는것이 아닌 깊이 테스트를 수행하여 AO Fields 사이즈의 직육면체와 모든 오브젝트의 렌더링이 끝난 씬과의 교차부분 ( AO Fields를 적용할수 있는 부분)을 구하는 것이 주된 목적이다.

이것은 Deferred 렌더링의 라이팅 방식과 꽤 닮은 형태이다. Deferred 렌더링의 라이팅 방식에서는「광원의 적용범위」를 구하지만 AO Fields에서는「차폐의 적용범위」를 구하고있는 것이다

실제로 렌더링을 수행한 픽셀 셰이더에서는 깊이 테스트의 결과로 그 부분이 AO Fields를 적용해야할 장소인가라고 판단가능한 경우는 그 깊이 값을 바탕으로 월드 좌표계의 위치정보를 역산하여 그 값으로부터 AO Fields의 어느 복셀의 영향 하에 있는가 ( 오브젝트의 로컬 좌표 )를 구한다.

AO Fields의 어느 복셀을 읽어내면 좋은가를 구하면, 그 복셀에 대응하는 3D 텍스처로부터 차폐 벡터와 차폐율을 읽어낸다. 다음은 그 장소의 법선벡터를 읽어내어( Defferd 렌더링 엔진이라면 깊이 버퍼와 함께 이전에 G 버퍼로써 렌더링이 끝난 상태) 이 방향벡터와의 사각 관계를 검토하면서 차폐율에 바이어스값을 주고 그림자색(陰色)을 산출하면 된다

여기까지의 내용을 실제로 실행한것이 오른쪽에 있는 스크린샷으로 아니나 다를까 엉성한 복셀단위로 관리되고있는 AO Fields의 내용이 사각형처럼 렌더링 결과에 여실히 나타나 버렸다。

【차폐도의 산출식】
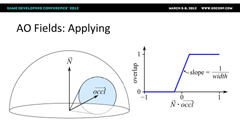해당 장소의 차폐도 산출식. Strength는 차폐강도를 나타내며 이것은 아티스트가 오브젝트마다 결정할 수 있다. 즉 AO Fields에 따라 그림자색陰色의 농담을 Strength로 컨트롤 할 수 있다(왼쪽)、해당 장소에 법선벡터가 차폐 벡터의 방향에 가까우면 가까울 수록 그림자색(陰色)은 짙어진다 라는 조정 항목이다（오른쪽）


■　AO Fields의 개량


가장 외곽부분 경계에 있는 복셀을향해 차폐율이 0으로 되도록 AO Fields를 조정. 이 슬라이드에서 alpha는 α채널에 저장되어있는 차폐율을 말한다
그래서 각 오브젝트의 AO Fields에 대해, 가장 외곽부분 경계에 있는 복셀의 차폐율을 강제적으로 0으로 하여 AO Fields의 차폐율을 가장 큰 값으로부터 외곽 복셀의 차폐율을 점점 0으로 선형적 감쇠형태의 조정을 한다. 이 조정을 수행하는 것이 이 스크린 샷으로 사각형처럼 보이는 아티펙트는 거의 알수 없게 된다.



【AO Fields 조정】
왼쪽이 조정 전 오른쪽이 조정 후. 사각형같이 보이는 아티펙트는 거의 보이지 않고 있다

하지만 아티펙트는 또하나 있다. 그것은 잘못된 그림자색(陰色)이 붙는다라는 아티펙트이다.
알기 쉬운 예로써 자동차의 본네트나 지붕, 사이드 스텝 부근에 불필요한 그림자색(陰色)이 생긴다.

이것은 AO Fields가 꽤 엉성한 복셀 단위로 계산되고있기 때문이며, 오브젝트의 경계면 부근에서는 차폐율이 급변하기 때문에 이 부근에서의 차폐율의 계산을 진행할때 많은 오차가 생겨 버리는 것이다

각 복셀로 차폐 항목을 계산할때에 이 복셀이 경계면에 있을때는 자동으로 차폐율을 조정하도록 하는AO Fields 계산법을 넣어보는 것도 생각해 봤지만 복잡한 형상이 있는 부분에서는 그것도 판단이 어려웠다.

그래서 어쩔수 없이 그림자색(陰色)을 입히는 픽셀 부분에 법선벡터를 참조하여 그 방향에 따라 AO Fields의 참조를 반 복셀 옆으로 땡겨서 조정(오프셋)을 더하는 방식을 채택했다

약간 강인한 대응책이긴 하지만 결과는 썩 좋았다. 경계면 부근에서의 의미불명한 그림자색(陰色)을 없애는데는 성공. 하지만 그 부작용으로써 차폐율이 높은 부분에서의 그림자색(陰色)이 보다 짙게 나와버리게 되었다. 뭐 그렇게 큰 문제는 아니라고 판단..

최종적으로는 이 방식을 채택하는 것으로 결정했다.. 여기까지 내용을 영상으로 종합한 것이 아래에 있는 영상이다


【AO Fields 조정 -2】
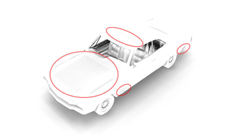경계면에서의 불필요한 그림자(陰)색。원으로 표시한 부분이 해당 부분이다（왼쪽）。셰이딩 대상 장소의 법선 벡터의 방향에 따라 반 복셀 빗겨서 AO Fields를 샘플링한 방식을 넣는 것으로 아티펙트를 제거（오른쪽）


■　AO Decals 이라는 발상~ 두께가 얇은 오브젝트를 위한 AO Fields


「inFAMOUS 2」에서는 창문이나 문 같은 두께가 엷은 오브젝트에 관해서는 보다 간략화한 모델의 AO Fields를 채택했다고 한다.

기본적인 방식은 AO Fields와 같으며 대상 오브젝트를 복셀 화 하여 구분하고 각 복셀 단위로 차폐 항목을 구해 나간다는 방식이지만 엷은 오브젝트이므로 대담하게 간략화 한것을 도입했다.

우선 3D 텍스처는 사용하지 않으며 AO 정보는 2D 텍스처로 다룬다. 그리고 복셀의 레이어는 4층으로 한정하고 첫번째 계층의 정보를 R 텍셀에 2,3,4계층의 정보를 각각의 G, B, α 에 저장한다.

각 수치가 스칼라로 되버리므로 AO Fields에 저장되어있던 차폐방향벡터는 버리고, 차폐율만을 저장하도록 하는 것이다. 이 오브젝트의 4계층분의 차폐율을 저장한 텍스처를 AO Decals라고 부른다

AO Decals에서는 차폐방향은 각 복셀에서 동일방향을 가리키고있다 라고 가정되버린다.
예를들면 창문이라면 벽에 붙어있으므로 차폐방향은 벽면으로부터봤을때 옥외 방향으로의 반구방향뿐이라고 생각한다 (반대측은 항상 벽으로 차폐되어 있다고 간주한다)

AO Decals에서도 사전계산으로써 차폐율 계산은 필요하지만 AO Fields에서 했던 각 복셀에서의 큐브맵 렌더링은 사용하지 않으며 보다 간략화한 알고리즘을 사용한다

대상 오브젝트를 텍스처에 하이트맵으로써 렌더링하고, 그 결과에 대해서 4계층분의 레이어로 구분짓고 각 계층의 각 텍셀에 대응하는 하이트맵의 높치값과 그 주변의 높이값을 검토하여 차폐율을 계산한다. 하이트맵을 깊이 버퍼로써 보면 이 방식은 SSAO와 거의 동일하다

SSAO 처리와 다른것은 공중에 뜬 지점에 대해서도 차폐율을 계산하는 점이다. 이 것은 창틀을 걸치는것 같은 제3의 오브젝트에 대해서도 그림자색(陰色) 입히도록 하기 위해서 일 것이다

【AO Decals -1】
AO Decals에서는 αRGB의 4텍셀을 4계층의 각 지점의 차폐율로 할당한다. 기본적인 사고는 AO Fields와 같지만 AO Decals에서는 차폐방향은 생략하고 복셀도 4계층으로 한정하고 있다（왼쪽）。오브젝트를 하이트맵으로써 렌더링. 이것에 대해 4계층을 잘라 각 지점에서의 차폐율을 구한다. 차폐방향은 오른쪽 그림에서 말하면 바로위에 반구방향에 대해서 구한다（오른쪽）

【AO Decals -2】
엷은 오브젝트라고는 해도 4계층은 꽤 엉성한 공간분할이 된다（왼쪽）。차폐율은 오브젝트의 표면상 각지점으로부터 수행된다. 결과는 각 지점에 가장 가까운 계층에 저장되어있는(파란점). 다른 물체로의 차폐에도 대응하기 위해 공중점에서도 차폐율을 계산한다(초록색 점)（오른쪽）。

「inFAMOUS 2」에서의 AO Decals 방식。AO Decals에서는ε=0.7로써 AO Fields보다도 작은 경계상자를 할당하고있다
AO Decal 의 크기도 AO Fields 때와 같이 각 오브젝트가 완전히 들어가 있으며 약간 크긴 하지만 AO Fields때보다도 크기는 작은편이다.

이것은 처리부하에 배려와 오브젝트의 두께가 애초에 엷기 때문에
그정도로 크게 하지 않아도 충분하기 때문일 것이다.

데이터 사이즈로써의 AO Decals는 각 변 64~128 텍셀 정도로 하고 저장하는 것이 스칼라 값의 차폐율 이므로 다소의 오차도 허용할수있다는 것으로 DXT5 압축을 적용하고 있다. 데이터 사이즈로써는 4~16KB이고 AO Fields와 동일하다. 그렇게 크지는 않다.

런타임에서의 AO Decals의 적용은 AO Fields와 완전히 똑같다. 각 오브젝트의 렌더링을 끝낸 씬에 대해 AO Decals 사이즈의 직육면체를 렌더링하여 구해진 교차 부분에서 AO Decals에 저장된 차폐율을 바탕으로 그림자색(陰色)을 입혀 나간다. AO Decals에서는 차폐방향이 간략화되어 존재하지 않으므로 AO Fields보다도 단순하다

단 씬과 AO Decals의 교차 부분의 깊이값에 대응하는 차폐율을 4계층의 슬라이스한 AO Decals의 1계층부터 읽어내는 것 뿐으로는 포인트 샘플링이 되어 지저분하게 되버린다. 따라서 몇가지의 텍스처 필터링을 도입할 필요가 있다. 하지만 단일 텍스처내에 있는 αRGB의 각 수치에 대해서의 필터링 처리라는 것은 하드웨어에서는 불가능하므로 각자 픽셀 셰이더프로그램측에서 수행할 필요가 있다

【AO Decals - 3】
차폐율과 차폐강도 값만으로 그림자색陰色을 결정한다（왼쪽）、AO Decals로부터 차에 위치를 가져올 때의 필터링 처리를 하는 셰이더 코드 예（오른쪽））


■　AO Decals의 개량


원으로 그린 부분이 하얀선의 아티펙트가...
라는 것으로 지금까지의 처리를 적용한 것이 오른쪽 스크린 샷이다.
그러나 벽면과 창틀의 교차 부분의 어렴풋이 하얀 선이 보이고 있다.

실은 이부분이 AO Fields에서도 보이지만 엉성한 복셀화의 폐해로
경계면에서의 급격한 차폐율 변화가 생기는 것이 원인이다.

구체적으로는 경계면안쪽이 차폐율 0이고 경계면 바깥쪽이 "높은" 차폐율일 경우에 텍스처 필터링의 효과에 의해 얻어낸 차폐율이 엷어져 버린다는 것으로 인해 생긴다

이것을 막기 위해서는 하이트맵에 숨어 있는 부분에 대한 경계면의 차폐율은 그 주변에 있는 하이트맵에 숨어있지 않은 경계면에 차폐율로 덮어 씌워 버리면 된다. 이것으로 경계면의 차폐율이 급격히 변하게 되지 않게 되어 하얀 선의 아티펙트를 사라지게 할 수 있다

파란색은 통상의 차폐율을 구한 점. 빨간점은 하이트맵에 숨어있는 특수한 점（왼쪽）、경계부근의 차폐율은 균일화해 버리므로 이 부근에서의 텍스처 필터링에 의한 차폐율의 급격한 변화를 회피한다（右）

해당 처리를 적용하기전（왼쪽）、하얀 선의 아티펙트가 사라짐（오른쪽）

위의 스크린샷은 실은 조금 결과를 미리 보여준 샷으로 실은 아직 벽면에 대해서 직교하는 오브젝트의 측면의 그림자색(陰色)이 부드럽게 되버린다는 아티펙트가 남아있다. 창문의 예를 들자면 마치 측면이 둥근형태를 띄고있는 것 같은 그림자색(陰色)이 되어 버린다는 것이다

이것에 관해서는 AO Decals를 더욱 개량하는것이 아닌 각 오브젝트 측에 배후의 무한으로 퍼지는 벽면 평면이 있다고 하고 각 버텍스의 부가정보로써 이 벽면으로부터의 차폐율을 새겨넣어버리는 것으로 대처한다. 즉 벽면에 직교한느 측면에 나오는 짙은 그림자색(陰色)은 AO Decals의 효과가 아닌 버텍스의 새겨넣은 AO의 효과 라는 것이다. 여기까지 내용을 영상으로 종합한 것이 아래의 영상이다



AO Decals 만으로는 이와 같은 측면에 그림자색(陰色)이 바로 위로 갈수록 엷어져 버려, 마치 둥근형태를 띄고있는 것 같은 음영이 보이게 되버린다（왼쪽）。그림 중간에 있는 식으로 구한 벽으로부터의 차폐율을 오브젝트의 각 버텍스에 새겨넣는 것으로 대처한다（오른쪽）



도입하기전（왼쪽）、도입한 결과。측면의 그림자색陰色이 확실히 나오게 되었다（오른쪽）


■　마치며~ AO Fields의 방식을 몸이 변형되는 인체에 적용하는 방법


이후에는 AO Fields 방식을 몸이 변형하는 인체같은 오브젝트에도 적용해 나가는 것을 과제로 하고 있다. 게다가 그것은 결코 꿈은 아니다
세션에 마지막에는「inFAMOUS 2」에서 AO Fields와 AO Decals을 도입함으로써 증가한 추가 텍스처 용량의 레포트가 공개되었다。

「inFAMOUS 2」에서는 이 AO Fields 나 AO Decals의 개념을 도입한 유니크 오브젝트는 119종이라고 하며 그것들의 총 텍스처 용량( AO Fields의 3D 텍스처와 AO Declas의 2D 텍스처의 합산용량)은 불과 569KB라는 것。

119개의 오브젝트에 대한 추가 텍스처 용량으로써는 그럭저럭의 증가량으로 이걸로 얻을 수있는 효과를 생각해보면 합리적인 대책이었다라고 할 수있겠다

퍼포먼스적으로는 1프레임당 평균적으로 봤을때 20~100개의 AO Fields, AO Decals의 렌더링 부하가 걸리고 있지만 소요시간은 PS3에서 0.3~ 1.0ms Worst Case라도 2.3ms였다라고 분석되고 있다. 기본적으로는 버텍스부하보다는 픽셀 부하가 높은 처리 이므로 표시 프레임에 대해서 이 방식에 의해 그림자색(陰色)이 그려지고 있을때에 크게 부하가 높아지는 것 같다.

AO Fields, AO Decals는 현재 오브젝트 자신이 변형되지 않는 자동차등의 대도구(大道具)오브젝트, 쓰레기통 같은 소도구(小道具)오브젝트에서 밖에 적용되고 있지 않다. 오브젝트가 움직여도 제대로 그 움직인 부분에다른물체의 차폐는 고려되지만, 손발이 움직이는 인체 같은 그 자체가변형되는 오브젝트에 관해서는 이 AO Fields, AO Decals는 대응하고 있지 않다. 이 부분이 이후 연구해 나가야 할 확장 방향성이라고 Reed씨는 말한다.

단,인체 같이 [ 자신이 변형하는 ] 오브젝트에 대해서의 AO Fields의 아이디어는 Reed씨도 기다리고 있으다.인체라면 팔, 다리, 목, 몸통 같은 주요 인체 구성 파츠를 분해하여 각각의 부위에 대해 AO Fields를 적용한다 같은 연구이다.
즉 변형하는 오브젝트를 변형하지않는 오브젝트의 집합체로써 처리해 준다라는 것이다.
이렇게 함으로써 추가 부하도 리니어 스케일로 어림잡는 것이 가능하다

SSAO를 발단으로 한 새로운 셰이딩 방식은 당분간은 앞으로도 진화를 보여줄 것이며 계속 유행해나갈 것이라고 필자는 생각한다.

AO Field와 AO Decals에 의한 추가메모리 사용량（왼쪽）과
추가 GPU 부하（오른쪽）


저작자표시 비영리 (새창열림)



원문 : http://wiki.gamedev.net/index.php/D3DBook:Screen_Space_Ambient_Occlusion
         
SSAO( Screen Space Ambient Occlusion )

http://bleedmin.blogspot.com/2012/04/ssao.html  

컴퓨터로 생성된 이미지에 사실성을 향상시키기 위한 방법들은 매우 많다. 그런 방법들 중 하나가 물체의 라이팅 방정식을 이용해 값을 구할때 그림자 효과를 계산하는 방법이다. 실시간 컴퓨터 그래픽에서 유용한 그림자 기법들은 매우 많으며, 그러한 각각 기법들은 장단점을 모두 보인다. 일반적으로, 그림자 기법들은 그림자 품질과 실행 효율 사이의 균형을 취하려 노력한다.

그런 기법들중 하나가 바로 SSAOScreen Space Ambient Occlusion라고 불리는 기법이다. 이 기법은 Martin Mittring이 2007 SIGGRAPH 컨퍼런스에서 발표한 논문 "Finding Next Gen"에서 처음 논의되었다. 이 알고리즘의 기본 컨셉은
전역 조명 과정Ambient lighting term을 장면의 한 점이 얼마나 차폐되는지를 구하는 기반으로 바꾸는 것이다. 이 방법이 AO의 컨셉을 처음으로 이용하는 기법은 아니지만, 이후의 장chapter에서 보게 되겠찌만 SSAO는 꽤나 현명한 추정과 단순함으로 매우 높은 성능을 유지하면서도 만족할만한 결과를 보여준다.

이 번 장에서는, SSAO의 배경이 되는 이론을 살펴보고, Direct3d 10 파이프라인을 이용하여 이 기법을 구현하는 방법을 제공하며, 성능과 품질의 향상을 위해 구현 단계에서 사용할 수 있는 파라미터들에 대하여 논의할 것이다. 마지막으로, 주어진 구현을 이용한 데모에 대하여 논의하여 이를 통해 알고리즘의 성능에 대해서 몇 가지 사항을 알리고자 한다.

알고리즘 이론

이제 우리는 SSAO의 유래에 관한 배경지식에 대해서 살펴보았으므로, 기법에 대하여 더욱 자세하게 살펴볼 준비가 되었다. SSAO는 단 하나의 단순한 명제를 사용함으로써 이전의 기법들과는 다른점을 보인다: SSAO는 이전에 레스터화되기 이전의 장면 정보를 사용하는 대신 현재 장면에서 주어진 점의 차폐의 양을 구하는데 오직 깊이 버퍼만을 이용한다. 이를 위해 깊이 버퍼를 직접적으로 사용하는 방법이나 깊이 정보를 보관하기 위해 특별한 렌더타겟을 생성하는 방법 모두 가능하다. 깊이 정보는 주어진 점의 주변점을 구하는 즉시 세밀하게 조사하여 그 점이 얼마나 차폐되었는지 계산하는데 사용한다. 차폐 인수occlution factor은 한지점에 얼마만큼의 전역광을 적용할것인지, 그 양을 조절하는데 사용한다.

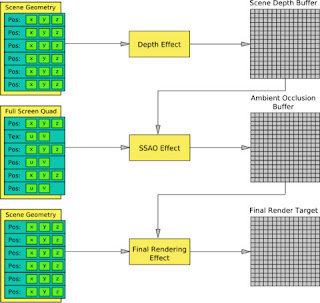
SSAO 알고리즘에서 사용하는 차폐 인수을 생성하는 방법은 논리적으로 두 단계 과정으로 이루어져 있다. 먼저 우리는 장면의 현재 시점을 기준으로 깊이 텍스처를 생성해야하고, 이 깊이 텍스처를 이용하여 현 장면의 최종 화면에서 각 픽셀의 차폐 정도를 결정한다. 이 과정은 아래의 그림 2에서 볼 수 있다.



그림2. SSAO 알고리즘의 개요
깊이 버퍼만을 사용하는 이 단순함은 성능과 품질면에서 몇가지 효과가 있다. 장면 정보가 렌더타겟으로 레스터화 하는 경우, 장면을 나타내는데 사용하는 정보가 3차원에서 2차원으로 줄어들게 된다. 데이터 축소는 매우 효율적인 명령을 제공하는 표준 GPU 파이프라인 하드웨어를 통해 수행된다. 또한 장면의 전체 차원을 줄임으로, 2D 장면 표현을 장면의 가시 영역으로 한정하여 이 프레임에 보이지 않는 물체에 대한 불필요한 연산을 제거할 수 있게 된다.

데이터 축소는 차폐 인수을 계산하는데 있어서 확실한 성능상의 이득을 제공하지만, 동시에 연산시에 필요한 정보 또한 제거한다. 이것은 우리가 계산으로 얻은 차폐 인수 값이 꼭 정확한 값이 아닐 수 있음을 의미하지만, 이후의 장에서 보게 되겠지만 전역 조명 과정은 근사치 일지라도 훌륭하게 장면의 현실감을 부여해 준다.

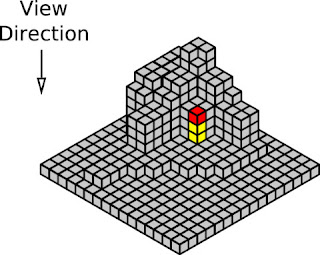
텍스처에 장면의 깊이 정보를 저장한 뒤, 깊이 값의 직접 인접에 기반하여 각 점이 얼마나 차폐되었는지 결정해야 한다. 이 연산은 다른 AO 기법들과 꽤나 비슷하다. 그림 3에 보이는 바와같이 깊이 버퍼를 고려해야한다 :


그림 3. 뷰view 방향이 아래쪽으로 향한 샘플 깊이 버퍼

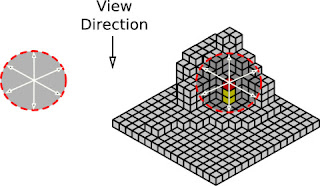
이상적으로 주어진 점을 중심으로 둘러싼 반지름 r인 구를 생성하고, 그 구와 깊이 버퍼에 있는 물체와 교차하는 부피를 구하기 구를 따라 통합해 나간다. 이 컨셉은 여기 그림 4에서 볼 수 있다.


그림 4. 차폐를 계산하기 위한 이상적인 샘플링 구

물론, 렌더된 이미지의 모든 픽셀에서 복잡한 3D 통합을 수행하는 것은 전적으로 비효율적이다. 대신, 이 구의 부피 내에 존재하는 3D 샘플링 커널을 이용하여 이 구를 추정할 것이다. 샘플링 커널은 명시된 지점의 깊이 버퍼를 살펴, 그 각 가상의 점이 깊이 표면에 의해 가려지는지 결정하는데 이용된다. 샘플링 커널의 예시는 그림 5에 나타나 있으며, 우리의 표면점에 어떻게 적용해야 하는지도 보여준다.


그림 5. 단순화한 샘플링 커널과 깊이 버퍼 내에의 위치

차폐 인수는 차폐가 발생한 샘플링 커널의 합으로 구할 수 있다. 구현 부분에서 살펴보겠지만, 이 개별적인 계산은 카메라부터의 거리, 차폐 지점과 기준점 간의 거리, 아티스가 지정한 비례축소 인수 등의 몇가지 다른 인수들에 따라 더 민감하게, 혹은 덜 민감하게 할 수 있다.
구현

알고리즘이 어떻게 기능하는지 이해했따면, 이제 구현하는 방법에 대해 논의해 보자. 알고리즘 이론 파트에서 논의했듯이, 장면의 깊이 정보가 담긴 소스가 필요하다. 간단하게 하기 위해, 우리는 깊이 정보를 저장하기 위해 서로다른 부동소수 버퍼를 사용할 것이다. 비록 조금 더 복잡할지는 모르겠지만, 더 효율적인 기법은 장면의 깊이 값을 얻기 위해 z-버퍼를 이용할 것이다. The following code snippet shows how to create the floating point buffer, as well as the render target and shader resource views that we will be binding it to the pipeline with: 

// 깊이 버퍼 생성
D3D10_TEXTURE2D_DESC desc;
ZeroMemory( &desc, sizeof( desc ) );
desc.Width = pBufferSurfaceDesc->Width;
desc.Height = pBufferSurfaceDesc->Height;
desc.MipLevels = 1;
desc.ArraySize = 1;
desc.Format = DXGI_FORMAT_R32_FLOAT;
desc.SampleDesc.Count = 1;
desc.Usage = D3D10_USAGE_DEFAULT;
desc.BindFlags = D3D10_BIND_RENDER_TARGET | D3D10_BIND_SHADER_RESOURCE;

pd3dDevice->CreateTexture2D( &desc, NULL, &g_pDepthTex2D ); 

// 렌더 타겟 리소스 뷰 생성
D3D10_RENDER_TARGET_VIEW_DESC rtDesc;
rtDesc.Format = desc.Format;
rtDesc.ViewDimension = D3D10_RTV_DIMENSION_TEXTURE2D;
rtDesc.Texture2D.MipSlice = 0; 

pd3dDevice->CreateRenderTargetView( g_pDepthTex2D, &rtDesc, &g_pDepthRTV ); 

// 셰이더-리소스 뷰 생성
D3D10_SHADER_RESOURCE_VIEW_DESC srDesc;
srDesc.Format = desc.Format;
srDesc.ViewDimension = D3D10_SRV_DIMENSION_TEXTURE2D;
srDesc.Texture2D.MostDetailedMip = 0;
srDesc.Texture2D.MipLevels = 1; 

pd3dDevice->CreateShaderResourceView( g_pDepthTex2D, &srDesc, &g_pDepthSRV );


깊이 정보를 생성한 후, 다음 단계는 최종 장면 내 각 픽셀의 차폐 인수를 계산하는 것이다. 이 정보는 두번째 단일 성분 부동소수 버퍼에 저장할 것이다. 이 버퍼를 생성하기 위한 코드는 부동소수 깊이 버퍼를 생성하기 위해 사용한 코드와 매우 유사하므로, 페이지 길이를 줄이기 위해 생략한다.

이제 두 버퍼가 모두 생성되었으므로, 각 버퍼에 저장할 정보를 생성하는 부분을 상세히 살펴보자. 깊이 버퍼는 뷰 공간의 깊이값을 기본적으로 저장한다. 절단 공간 깊이clip space depth 대신 선형 뷰 공간 깊이linear view space depth를 사용하여 투시 투영perspective projection으로 인한 깊이 범위 왜곡을 방지한다. 뷰 공간 깊이는 입력 버텍스와 월드뷰world-view 행렬을 곱해서 구할 수 있다. 그런뒤 뷰 공간 깊이는 단일 성분 버텍스 속성으로 픽셀 셰이더로 전달된다. 

fragment VS( vertex IN )
{
    fragment OUT;
    // 절단 공간 좌표를 출력
    OUT.position = mul( float4(IN.position, 1), WVP );
    // 뷰 공간 좌표를 계산
    float3 viewpos = mul( float4( IN.position, 1 ), WV ).xyz;
    // 뷰 공간 깊이값을 저장
    OUT.viewdepth = viewpos.z;
    return OUT;
}


깊이값을 부동소수 버퍼에 저장하기 위해, 픽셀 셰이더에서는 근거리 클리핑 평면과 원거리 클리핑 평면간의 거리에 따라 깊이값을 확대/축소한다. 이것은 범위 [ 0, 1 ]을 가진 선형, 정규화된 깊이 값을 생성한다. 

pixel PS( fragment IN )
{
    pixel OUT;

    // 뷰 공간 범위에 따라 깊이값을 확대/축소
    float normDepth = IN.viewdepth / 100.0f;

    // 확대/축소된 값을 출력
    OUT.color = float4( normDepth, normDepth, normDepth, normDepth );

    return OUT;
}


저장된 정규화된 깊이 정보를 가지고, 각 픽셀의 차폐 인수를 생성하기 위해 깊이 버퍼를 셰이더 리소스로 바인딩하고 각 차폐 버퍼에 저장한다. 차폐 버퍼 생성은 단일 전체 스크린 화면을 렌더링함으로써 초기화한다. 전체 스크린 화면의 버텍스들은 단지 단일 2-성분 속성을 가지고 있으며, 이는 깊이 버퍼 내의 자신의 위치에 대응하는 텍스처 좌표를 나타내고 있다. 버텍스 셰이더는 단순히 이 파라미터들을 픽셀 셰이더에 전달만 한다.

fragment VS( vertex IN )
{
    fragment OUT;
    OUT.position = float4( IN.position.x, IN.position.y, 0.0f, 1.0f );
    OUT.tex = IN.tex;

    return OUT;
}


필셀 셰이더는 3D 샘플링 커널의 형태를 3-성분 벡터의 배열로 정의하는 것으로 시작한다. 벡터의 길이는 [ 0, 1 ] 범위 사이에서 다양히 변하며 각 차폐 테스트에서 약간의 변화를 주게 된다.

const float3 avKernel[8] ={
    normalize( float3( 1, 1, 1 ) ) * 0.125f,
    normalize( float3( -1,-1,-1 ) ) * 0.250f,
    normalize( float3( -1,-1, 1 ) ) * 0.375f,
    normalize( float3( -1, 1,-1 ) ) * 0.500f,
    normalize( float3( -1, 1 ,1 ) ) * 0.625f,
    normalize( float3( 1,-1,-1 ) ) * 0.750f,
    normalize( float3( 1,-1, 1 ) ) * 0.875f,
    normalize( float3( 1, 1,-1 ) ) * 1.000f
}


다음으로, 픽셀 셰이더는 텍스처 룩업 내에서 샘플링 커널을 반사시키기 위한 렌덤 벡터를 찾는다. 이것은 사용한 샘플링 커널을 이용해 매우 다양한 변화를 줄 수 있으며, 이는 적은 수의 차폐 테스트를 하더라도 높은 수준의 결과를 제공할 수 있게 해준다. 이는 차폐를 계산하기 위한 깊이를 효과적으로 "흐트려jitter" 주어, 우리가 현재 픽셀의 주변 공간을 언더샘플링 한다는 사실을 숨겨준다.

float3 random = VectorTexture.Sample( VectorSampler, IN.tex.xy * 10.0f ).xyz;random = random * 2.0f - 1.0f;


이제 픽셀 셰이더가 현제 픽셀의 깊이값을 바탕으로 샘플링 커널에 적용하기 위한 확대/축소값을 계산할 것이다. 이 픽셀의 깊이값은 깊이 버퍼로부터 읽어들여 근거리 평면과 원거리 평면간의 거리를 곱함으로 뷰 공간으로 도로 확장된다. 그런 뒤 샘플링 커널의 x 와 y 성분을 위한 확대/축소값을 계산하는데, 이는 샘플링 커널의 희망 반지름( 미터 단위 )을 픽셀의 깊이값( 미터 단위 )로 나누면 된다. 이는 개별 샘플을 찾기위해 사용되는 텍스처 좌표를 확대/축소한다. z 성분의 확대/축소값은 희망 커널 반지름을 근거리 평면과 원거리 평면간의 거리로 나누어 구할 수 있다. 이는 모든 깊이값의 비교를 우리가 깊이 버퍼에 저장한것과 같은 정규화된 깊이 공간에서 이루어지도록 하게 해준다.

float fRadius = vSSAOParams.y; 
float fPixelDepth = DepthTexture.Sample( DepthSampler, IN.tex.xy ).r;
float fDepth = fPixelDepth * vViewDimensions.z;
float3 vKernelScale = float3( fRadius / fDepth, fRadius / fDepth, fRadius / vViewDimensions.z );


커널 확대/축소값이 구해지면, 개별 차폐 테스트를 수행할 수 있게 된다. 이것은 for 루프 내에서 샘플링 커널이 가르키는 각 점들을 계속해서 반복하는 것으로 이루어진다. 현재 픽셀의 텍스처 좌표는 렌덤하게 반사된 커널 벡터의 x와 y 성분을 통해 차감 계산되고 새 좌표에서 깊이값을 살펴보기 위해 사용된다. 이 깊이 값은 커널 벡터의 z 성분을 통해 차감 계산되고 현재 픽셀의 깊이와 비교된다. 

float fOcclusion = 0.0f; 
for ( int j = 1; j < 3; j++ )
{
    float3 random = VectorTexture.Sample( VectorSampler, IN.tex.xy * ( 7.0f + (float)j ) ).xyz;
    random = random * 2.0f - 1.0f;

    for ( int i = 0; i < 8; i++ )
    {
        float3 vRotatedKernel = reflect( avKernel[i], random ) * vKernelScale;
        float fSampleDepth = DepthTexture.Sample( DepthSampler, vRotatedKernel.xy + IN.tex.xy ).r;
        float fDelta = max( fSampleDepth - fPixelDepth + vRotatedKernel.z, 0 );
        float fRange = abs( fDelta ) / ( vKernelScale.z * vSSAOParams.z );
        fOcclusion += lerp( fDelta * vSSAOParams.w, vSSAOParams.x, saturate( fRange ) );
    }
}


깊이값의 델타값( = 차이값 )은 어플리케이션의 선택가능한 범위값으로 정규화된다. 이것은 깊이값 차이의 관계 등급을 결정하기 위한 인수를 생성하기 위함이다. 차례로, 이 정보는 이 특정의 차폐 테스트의 범위를 수정할 수 있다. 예를 들어, 한 물체가 장면의 전경에 위치하고 다른 하나의 물체가 그 뒤에 부분적으로 가려져 있다면, 전경의 물체가 유일한 차폐물인 경우 뒷쪽 물체를 위해 불필요한 차폐 테스트를 계산할 필요가 없다. 반대로 배경의 물체에는 앞 물체의 가장자리를 따라 그림자 같은 후광이 나타날 것이다. The implementation of this scaling is to linearly interpolate between a scaled version of the delta value and a default value, with the interpolation amount based on the range value. 

fOcclusion += lerp( ( fDelta * vSSAOParams.w ), vSSAOParams.x, saturate( fRange ) );


최종 픽셀 색상을 내놓기 전의 마지막 단계는 모든 커널 샘플로부터 평균 차폐값을 계산하고, 그 값을 최대/최소 차폐 값 사이를 보간하는데 사용하는 것이다. 이 마지막 보간은 광범위한 차폐값을 압축해주고 보다 부드러운 출력을 제공해준다. 이 장의 데모 프로그램에서 주의할 것은, 사진의 차폐를 계산하는데 단지 16샘플만을 사용했다는 것이다. 만일 더 많은 샘플을 사용했다면, 출력 차폐 버퍼는 더 부드러운 결과를 보여줄 것이다. 이것은 다른 등급의 하드웨어들에서 성능과 품질을 조정하는 좋은 방법이 된다.

OUT.color = fOcclusion / ( 2.0f * 8.0f ); 

// 범위 재매핑
OUT.color = lerp( 0.1f, 0.6, saturate( OUT.color.x ) );


생성한 차폐 버퍼를 가지고, 최종 렌더링 패스에서 셰이더 자원에 포함해 이를 이용할 수 있다. 렌더된 기하는 단수히 스크린 공간 텍스쳐 좌표를 계산하고, 차폐 버퍼를 샘플링한 뒤, 그 값을 이용하여 ambient 조건을 조정하면 된다. 예시로 제공되는 파일은 단순히 다섯 샘플의 평균을 이용하는 방법을 사용하였지만, 가우시안 브럴와 같은 좀더 세련된 방법을 대신 사용하는 것도 좋다.


SSAO 데모
데모 다운로드 : SSAO_Demo

이번 장을 위해 만든 데모 프로그램은 단순히 다수의 정방면체를 우리의 SSAO 셰이더만을 이용하여 렌더링한 것이다. 이번 기법에서 논의된 조절가능한 파라미터들에 대해서는 화면상의 슬라이더 콘트롤러를 이용하여 실시간으로 바꿀 수 있다. 그림 6 이하는 차폐 버퍼의 모습과 최종 출력 렌더링의 결과를 볼 수 있다. 한가지 알릴 사실은 차폐 효과를 보다 과장하기 위하여 차폐 파라미터들을 조절했다.


그림 6. 데모 프로그램의 차폐 버퍼의 모습

그림 7. 데모 프로그램의 최종 출력 렌더링의 모습

결론

In this chapter we developed an efficient, screen space technique for adding realism to the ambient lighting term of the standard phong lighting model. This technique provides one implementation of the SSAO algorithm, but it is certainly not the only one. The current method can be modified for a given type of scene, with more or less occlusion for distant geometry. In addition, the minimum and maximum amounts of occlusion, interpolation techniques, and sampling kernels are all potential areas for improvement or simplification. This chapter has attempted to provide you with an insight into the inner workings of the SSAO technique as well as a sample implementation to get you started.




저작자표시 비영리 (새창열림)




일반적인 game scene 에서의 SSAO 요소.

SSAO 와 diffuse lighting 을 비교. 

Screen Space Ambient Occlusion( SSAO ) 는 이미 잘 알려진 ambient occlusion 이라는 효과를 실시간에 효율적으로 근사계산하기 위한 rendering 기법입니다. 이것은 Crysis 라는 PC game 에서 2007 년에 처음 사용되었습니다.

이 algorithm 은 순수하게 computer 의 GPU 상에서 실행되며, texture 에 저장된 scene depth buffer 를 분석함으로써 pixel shader 로서 구현됩니다. 화면상의 모든 pixel 에 대해서 pixel shader 는 현재 pixel 주변의 깊이값들을 sampling 하고 sampling 된 각 point 로부터 occlusion 의 총합을 게산하려고 시도합니다. 가장 단순한 구현에서는 occlusion factor 는 현재 point 와 sampling 된 point 사이의 깊이 차에만 의존합니다.

부가적인 세련된 방식을 사용하지 않는다면 그러한 막무가내식( brute force ) 기법은 좋은 가시 품질을 위해 pixel 당 약 200 번의 texture read 를 요구할 것입니다. 이것은 현대의 graphic hardware 상에서 실시간 rendering 에 적합하지 않습니다. 더 적게 read 하면서 더 좋은 결과를 얻기 위해서 sampling 은 무작위적으로 회전되는 kernel 을 사용해 수행됩니다. 최종 이미지에서 high-frequency noise 만을 획득하기 위해서 이 kernel orientation 은 모든 N screen pixel 들에 대해 반복됩니다. 마지막으로 이러한 high freqency noise 들은 NxN 크기의 후처리 blurring 단계에서 거의 대부분 제거되는데 깊이 불연속성을 고려하게 됩니다( 인접한 normal 과 dpeth 를 비교하는 것과 같은 기법을 사용하게 됩니다 ). 그러한 방식은 pixel 당 16 개 혹은 그 이하의 깊이 sample 을 사용해 고품질의 결과를 얻을 수 있게 해 주며, 기본적으로 computer game 과 같은 실시간 응용프로그램에서 SSAO 를 사용할 수 있게 해 줍니다.

다른 ambient occlusion 방식과 비교해 SSAO 는 다음과 같은 이점을 가집니다 :
  • Scene 복잡도에 독립적.
  • Data 에 대한 전처리, loading time, system memory 할당을 필요로 하지 않음.
  • 동적 scene 에서 잘 동작함.
  • 화면상의 모든 pixel 에 대해 동일한 방식이 적용됨.
  • CPU 를 사용하지 않음 - 온전히 GPU 상에서 실행됨.
  • 현대 graphics pipeline 과 쉽게 통합됨.
물론 단점도 가지고 있습니다 :
  • Rather local and in many cases view-dependent, as it is dependent on adjacent texel depth which may be generated by any geometry whatsover.
  • 개체의 모서리 같은 곳에서 깊이 불연속성을 저해하지 않고 올바른 smooth/blur 를 하기 어렵다( the occlusion should not "bleed" onto objects ).
See also
Externel links


저작자표시 비영리 (새창열림)



컴퓨터에서는 같은 1234 라고 해도, 문자열로서의 1234 일 수도 있고, 진짜 숫자로서의 1234 일 수도 있습니다.

문자로서의 숫자를, 진짜 숫자로 바꾸어서 연산을 할 수 있게 해주는 함수들입니다.

atoi() : String To int


문자로 된 숫자를, 진짜 숫자의 정수로 변환
#include
#include

int main() {
  int num;
  char *s = "1234.9999";

  num = atoi(s);
  printf("문자 = %s\n숫자(int) = %d\n", s, num);

  return 0;
}


실행 결과:
문자 = 1234.9999
숫자(int) = 1234

만약 문자열에 소수점이 있다면 반올림하지 않고 소수점 이하를 무조건 무시합니다. 에러가 난다면 0을 반환합니다.
그래서 위의 소스가 만약 char *s = "ABCD"; 이렇게 되었다면 "숫자(int) = 0" 으로 출력됩니다.

atoi() 함수는 stdlib.h 에 정의되어 있습니다.



atol() : String To long


int 가 아닌 long형 정수로 변환할 때는 atol()을 사용합니다.
#include
#include

int main() {
  long num;
  char *s = "98765432";

  num = atol(s);
  printf("문자열 = %s\n숫자(long) = %ld\n", s, num);
  return 0;
}


실행 결과:
문자열 = 98765432
숫자(long) = 98765432



atof() : String To double


문자로 된 숫자를, 진짜 숫자의 실수로 변환
#include
#include

int main() {
  double f;
  char *s = "12345.67";

  f = atof(s);
  printf("문자열 = %s\n실수(double) = %0.3f\n", s, f);

  return 0;
}


실행 결과:
문자열 = 12345.67
실수(double) = 12345.670

atof() 함수는 double형 실수를 반환합니다. 그래서 이것을 float형 실수로 받으면
warning C4244: '=' : conversion from 'double' to 'float', possible loss of data
이런 경고가 나오게 됩니다.




▶▶ [C언어] 숫자(정수;int, long, unsigned long)를 문자열로 변환하는 함수 - itoa()

▶▶ [C언어] 숫자(실수;float)를 문자열로 변환하는 함수 - sprintf()



16진수 문자열을 숫자로 변환: ▶▶ C언어] 헥사(HEX; 16진수) 문자열을, 10진수 정수 숫자로 변환 함수; Hex String to Int Number

2진수 문자열을 숫자로 변환: ▶▶ C언어] 2진수 문자열을, 10진수 정수 숫자로 변환 함수; Base-2 String to Int Number


저작자표시 비영리 (새창열림)


오늘은 아주 아주 짧고, 간단한 내용 하나 적어볼까 합니다.

스마트폰에 대해서, 열풍이 불길래, 아주 잠깐, 옛날 기억을 살려서, OpenGLES용 렌더러를 살짝 만들어본적이 있는데요. 그 때, 렌더링 파워가 어느 정도까지 될까? 라는 궁금증이 있었는데, 마침 "인피니트 블레이드"라는 게임이 출시되어서, "아~ 이 정도는 되는구나!"라고 생각했었죠.

특히, 스펙큘러가 반짝 반짝 하는 것을 보고, PC에서 하는 것 처럼 했을까? 라는 생각이 들었었는데, 좀 찾아보니까, 고정 테이블을 이용한 방법이 있더군요. 살짜쿵 소개해볼까 합니다. (실제로 UDK의 모바일 셰이더를 열어보니, 요게 있더군요.)

일반적인 Specular 계산



view plaincopy to clipboardprint?
  1. float BaseSpec = max(0, dot(normal, halfvector));  
  2. // SpecPower = 8, 16, 32, ...  
  3. float3 Specular = pow(BaseSpec, SpecPower);   
PC에서도 아깝지만, 스마트폰에서 pow(x, 32)를 하면 완전 아깝죠... (실제 테스트는 안해봤어요!)pow(x, n)을 이미 테이블로 만들어 놓은 값을 참고해서, max(A * x + B)로 만들 수가 있습니다.
view plaincopy to clipboardprint?
  1. float BaseSpec = max(0, dot(normal, halfvector));  
  2. // N = 18, M = 2  
  3. #define SpecA 6.645  
  4. #define SpecB -5.645  
  5. float SpecularAmount = clamp( SpecA * BaseSpec + SpecB, 0, 1 );  
  6. float3 Specular = BaseSpec * SpecularAmount;  
A와 B는 이미 만들어진, 아래 테이블을 참조하여, 결정하면 됩니다.
(UDK를 보면, M=2일 때 보기가 좋다고 하네요...) 




이게 끝입니다. ㅎㅎ 간단하죠!

이 처럼 지수 계산을 간단한 곱셈으로 줄일 수 있어서, 스펙큘러를 사용하면서도 최적화를 할 수 있습니다. (결국, mad_sat instruction 하나로 처리가 가능!)
(물론, 오차 범위나 결과의 차이는 고려해야 합니다.)

그럼 어떤 차이가 있는지 한번 볼까요? 
(개인 학습용으로 개발된 렌더러에서 붙여보았습니다.)

[pow(n, 32)의 경우]
[N=18, M=2 테이블을 이용함]
직접적인 비교는 어렵긴한데, 대충 어느 정도 차이가 나는지를 보실 수는 있을 것입니다. 너무 하이라이트가 강하게 나오는 듯 하니, M, N을 테이블에서 바꾸보면서 테스트 해보면 될 듯 합니다.

간략하게 글을 썼습니다. 원본글을 읽어보시면, 더 도움이 되실거에요. (http://www.gamasutra.com/view/feature/2972/a_noninteger_power_function_on_.php)
사실, PC로 개발할 때에는 이 정도 비용은 크게 신경을 쓰지 않습니다. 하지만, 최근 게임들이 다양한 PC 사양에서 돌아가게 만들도록 옵션들을 다양하게 제공합니다. 심지어는 라이팅을 완전히 하지 않는 경우도 있지요.
생각해보면, 지수 연산을 마구 쓰기시작한지는 얼마 되지 않았습니다. 리니지2 정도의 시절?만 하더라도, Pixel 라이팅 자체를 거의 사용하지 않았으니까요. (이 때는 GlossMap으로 후려쳤지요!) 그러니, 당연하다고 하기에
는 생각보다 꽤 비싼 연산입니다.


저작자표시 비영리 (새창열림)

출처 : http://blog.naver.com/elsacred/50015540325

0. 들어가며

드디어 게으름을 떨치고 tangent space 에 대해서 정리해 봅니다.

이사도 했고 좀 더 여유가 생길 것 같습니다. 이제 좀 열심히 해 볼까 합니다.

픽셀 당 조명을 다루면서 탄젠트 공간에 대해 다루겠다고 이야기했었습니다.

저도 잘 모르지만 한 번 정리해 보도록 하겠습니다.

1. What is tangent space?

만약 우리가 구(sphere)인 메시를 가지고 있고 각 정점의 법선을 알고 있다고 할 때, 이것을 (텍스처) 평면상에 펼친다면 어떨까요. 각 점에서는 수직인 벡터들이었지만 평면에서 볼때는 위쪽을 가리키지 않고 서로 다른 방향을 가리키게 될 것입니다.


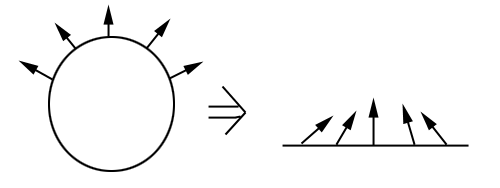
하지만 일관성을 위해서 평면으로 펼친 모든 normal 벡터가 위쪽을 바라보게 만든다면 어떻게 될까요. 그렇게 되면 각 점의 normal 벡터를 수직축으로 하는 좌표계가 생성이 됩니다.

normal(법선) 벡터는 어떠한 면에 수직인 벡터이며, bi-normal(종법선) 벡터는 이 normal 에 수직인 벡터입니다. 어떤 벡터 A, B, N 이 있을 때 T X B = N 인 관계의 두 벡터 A, B 를 접선이라고 합니다. X 는 외적기호구요. 이때 B 를 bi-normal 이라고 하면 T 를 tangent 라고 할 수 있습니다. 즉 T 와 B 는 같은 평면상에 존재하는 벡터라는 것을 알 수 있습니다.

즉 tangent space 라는 것은 오브젝트 공간에 있는 어떤 점의 normal 을 수직축으로 하는 공간이라고 할 수 있습니다.

탄젠트 공간을 개념도로 표현해 보면 아래와 같습니다.


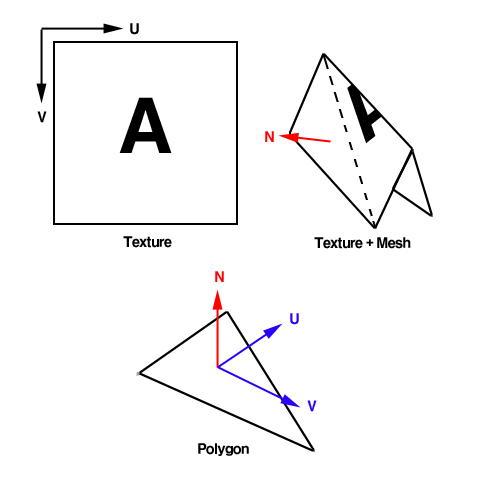
A 라는 그림이 그려진 텍스처를 메시에 입혔을 때, 어떤 텍셀의 normal N 은 U 및 V 방향의 벡터와 위와 같은 관계를 가집니다. 이 그림을 보면 외적( Cross )을 연상하실 수 있을 것입니다. 위의 tangent space 에서는 normal 이 항상 점에 있어서 수직인 방향( y )을 가리킨다고 언급했습니다. 관계를 나타내자면 U X V = N 입니다. 위에서 접선을 언급했는데 U 나 V 가 T 나 B 의 역할을 하게 되는 것입니다.

2. How to calculate tangent space

이제 실제로 이를 계산하는 방법에 대해서 살펴 보도록 하겠습니다. 우리는 오브젝트 공간에서 XYZ 를 축으로 하는 좌표계를 생성합니다. 하지만 위에서 언급했듯이 텍스처 공간에서는 이를 UVN 을 축으로 하는 좌표계로 변환하게 됩니다.
2.1. Plane equation
오브젝트 공간에 어떤 삼각형이 있다고 가정합니다. 그 삼각형의 한 점 Q( px, py, pz ) 가 있고 P0( x0, y0, z0 ) 라는 점의 좌표를 안다고 가정합니다. 그리고 N( a, b, c ) 를 안다고 가정합니다.

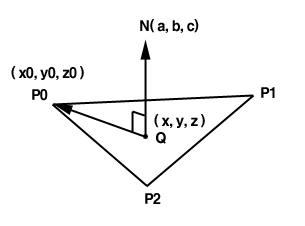
Q -> P0 를 P' 라고 할 때, P' 와 N 은 수직입니다. 이것이 의미하는 바는 둘을 내적한 결과가 0 이 나온다는 것입니다. 그렇다면 다음과 같은 평면 방정식을 유도할 수 있습니다.

dot( P', N ) = 0 -------------------------------- 1)

p' = ( ( x0 - x ), ( y0 - y ), ( z0 - z ) ) -------------------------------- 2)

N = ( a, b, c ) -------------------------------- 3)

dot( P', N ) = ( x0 - x )a + ( y0 - y )b + ( z0 - z )c -------------------------------- 2), 3) 에 의해

-( ax + by + cz ) + ( ax0 + by0 + cz0 ) = 0 -------------------------------- 1) 에 의해

ax + by + cz - ( ax0 + by0 + cz0 ) = 0 -------------------------------- 양변에 -1 곱함

a, b, c, x0, y0, z0 을 알고 있으므로 - ( ax0 + by0 + cz0 ) 은 상수이며 이를 D라 표현합니다.

ax + by + cz + D = 0 --------------------------------- 결론)

이 평면 방정식은 오브젝트 공간의 XYZ 축을 이용해 평면 위에서의 어떤 점의 좌표를 표현한 것입니다.

'평면' 이라는 단어를 통해서 약간이 느낌이 오실 겁니다. 우리는 오브젝트 공간의 어떤 벡터( normal )를 탄젠트(텍스처) 공간으로 옮기려고 하고 있습니다. 그렇다면 XYZ 관계 축으로 구성된 공간을 UNV 관계 축으로 구성된 공간으로 표현해야 한다는 것을 알 수 있습니다.

2.2. Drive a 3x3 matrix for tangent space

이제 개념적으로 탄젠트 공간이라는 것이 대충 이해가 가실테지만 문제는 여기부터입니다. 우리는 텍스처( normal map ) 에 normal 을 저장하게 됩니다. 이 때 그 값을 기울기( gradient )라는 용어로 표현을 많이 합니다. 기울기값은 당연히 오브젝트 공간의 normal 을 탄젠트 공간의 normal 로 저장한 값을 의미합니다.


위의 그림에서 P 는 오브젝트 공간에서의 정점이며, C 는 각 정점에 해당하는 텍스처 공간의 점들이라고 가정합시다.
다음과 같은 전제를 해 보겠습니다.
E0 : C0 에서 C1 으로 가는 벡터, 모서리 0
E1 : C0 에서 C2 로 가는 벡터, 모서리 1
우리가 위에서 계속 이야기한 것은 바로 y 축이 항상 위쪽을 바라보고 있다는 것입니다. 즉 y 값을 알고 있다는 것이죠. 그렇다면 E0 과 E1 을 사용하여 외적 계산을 하면 점 C0 의 노멀 벡터, 즉 Y 축 방향 벡터를 구할 수 있어야 함을 의미합니다.
E0 를 ( E0.u, E0.y, E0.v ) 라고 가정한다
E1 을 ( E1.u, E1.y, E1.v ) 라고 가정한다.

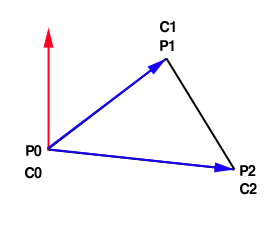
[출처] [본문스크랩] (작업중)탄젠트 공간(tangent space)|작성자 아도겐

저작자표시 비영리 (새창열림)

1. 탄젠트 공간이란?

우리 지구본이 있다고 하자. 그리고 이 지구본을 쫙 펼쳐 지도를 만들었다고 하자. 그런데 갑지가 다시 지구본이 필요해져 지도를 다시 지구본으로 만들어야 한다고 하자. 이 경우 우리는 어떻게 하면 지구본을 다시 만들 수 있을까?

비록 완벽하게 대응되는 것은 아니지만 위의예가 탄젠트 공간이 필요한 이유를 가장 잘 설명해 줄 수 있다. 만약 우리가 어떠한 3차원 물체를 2차원 평면으로 만들었다면, 우리는 이 2차원 평면을 바탕으로 3차원의 물체를 절대로 만들 수 없다. 하지만 3차원 물체를 2차원 평면으로 변환할때, 2차원 평면의 각 점에 그것이 3차원에서 가졌던 어떠한 정보를 저장해 두었다면 어떠한가? 이 경우 우리는 어떻게든 2차원 평면을 다시 3차원 물체로 복원할 수 있게 될 것이다. 여기서 말하는 어떠한 정보가 바로 탄젠트 space이다.

2. 탄젠트 공간의 정의

3차원 공간의 탄젠트 공간은 다음의 세 벡터를 축으로 하는 공간이다.

1) 한 점의 법선 벡터

2) 한 점의 접선(탄젠트) 벡터

3) 바이노멀 벡터 : 법선 벡터와 접선 벡터를 외적하면 구해지는 벡터

일반적으로 tangent space는 원래의 공간과 같은 차원을 가지며, 한 점에서 생성 가능한 모든 접선 벡터를 포함한다. 가령 위 그림의 경우, 접선 벡터와 바이노멀 벡터가 생성하는 평면은 가능한 모든 접선 벡터를 포함한다. 여기서 주의할 점은 tangent space의 개념은 비단 3차원 공간만이아닌 임의의 차원의 공간에 대해서도 적용될 수 있다는 점이다.

3. 탄젠트 번들

또한 모든 tangent space들은 2배의 dimension을 갖는 새로운 공간을 생성하기 위해 서로 붙여질 수 있는데(“glued together”), 이를 가능하게 해주는 것이 바로 tangent bundle의 개념이다. 이에대한 개념은 형태학 및 manifold등의 개념을 이해하여야 하므로 자세한 설명은 생략 하기로 한다.

4. 왜 사인, 코사인이 아닌 탄젠트를 이용하는가?

한점의 기울기를 가장 직관적으로 구할 수 있는 것이 다름아닌 탄젠트 이기 때문이다.

가령, 우리가 한 점의 기울기를 구해야 한다고 하자. 우리는 일반적으로 먼저 한 점의 접선을 빗변으로 하는 직각 삼각형을 생성하여야 하고, 그 직각 삼각형의 '높이/밑변' 으로 기울기를 구해주게 된다. 그런데 이 기울기는 바로 직각 삼각형의 빗변에 대응하는 각도의 탄젠트 값이다. 즉 탄젠트(빗변의 대응각)가 곧 기울기란 말이다. 때문에 한점의 기울기가 탄젠트라 불리기도 하는 것이다.

저작자표시 비영리 (새창열림)

+ Recent posts

티스토리툴바